Source Code Extended Euclidean Algorithm

Pada posting sebelumnya saya membahas, source code mendapat jumlah modulus 26 dengan turbo c++. Kali ini Source Code Extended Euclidean Algorithm, ini digunakan untuk menghitung invers dari sebuah bilangan dalam modulo n.

Extended Euclidean Algorithm :

1. Pilih sembarang d dalam range (max(p,q), Ø(n) -1)
2. GCD(d, Ø(n)) = 1
3.  n = p*q;  dimana p dan q adalah dua buah bilangan prima berbeda
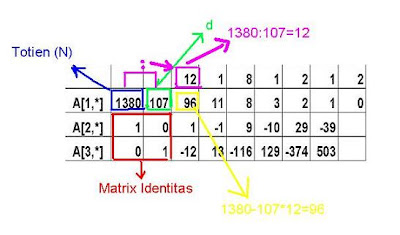
4. Bentuk Array A[3x2] dimana A[1,1] = Ø(n) dan A[1,2] = d
5. Isikan A[2,1] .. A[3,2] dengan matriks Identitas
6. Hitung bilangan bulat m dengan kondisi m * A[1,2] £ A[1,1];  usahakan m maksimum
7. Hitung X = A[1,1] - m * A[1,2] Ubah nilai A[1,1] = A{1,2] dan A[1,2] = X
•Lakukan langkah 4 dan 5 untuk baris kedua dan ketiga dari array A
•Ulangi langkah 3 sampai 5 hingga elemen terakhir dari baris 1 = 0
•Jika A[3,1] ³ 0 maka e = A[3,1] sebaliknya e = A[3,1] + Ø(n)

contoh :

Mis :
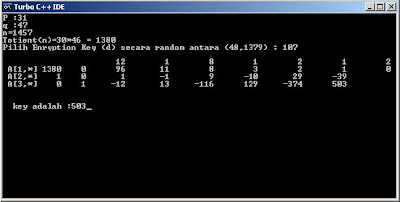
p = 31; q = 47 è n = 31.47 = 1457 ;   
Ø(n) = 30.46 =1380
Pilih d secara random dalam range (48,1379);
Mis : d = 107
e º d-1 mod (Ø(n))


Jawab :
pastikan GCD(31,47)=1;

untuk memastikan, anda bisa buka microsoft excel :

klik sembarang kolom, lalu ketikkan GCD(31,47), lalu klik sembarang kolom yang lain, jika hasilnya 1, maka nilai itu bisa digunakan.

  Perhatikan nilai tabel di atas :


12 = 1280 :107

96 = 1380-107*12

kenapa 1380-107*12 = 96 dan bukan 14196

Dalam dunia komputer, melakukan perhitungan memiliki tingkatan yaitu :

1. Perkalian dan pembagian
2. Penjumlahan dan pengurangan

seperti kasus di atas:

1380-170*12 = 96
Proses pertama yang dilakukan komputer adalah 1870*12 = 1284 kemudian 1380 - 1284 = 96


proses tersebut berlaku untuk semua kolom ;

Note : Semua Bilangan yang menghasilkan pecahan, dibulatkan kebawah

berikut source code untuk Extended Euclidean Algorithm di atas :

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106

#include<conio.h> #include<stdio.h> void main() { clrscr(); int p,q; long int totient_n; int angka_random; int x=2,y=5; int n; printf("P :"); scanf("%d",&p); printf("q :"); scanf("%d",&q); n=p*q; totient_n=(p-1)*(q-1); printf("n=%d",n); printf("\nTotient(n)=%d*%d = %ld",p-1,q-1,totient_n); do { gotoxy(x,y-1);printf("\nEnryption key (d) random antara (%d,%ld) : ",q+1,totient_n-1); scanf("%d",&angka_random); y=y+1;/* mengatasi posisi hasil saat terjadi kesalahan memasukkan angka random, sehingga posisi hasil tetap dibawah*/ }while(angka_randomtotient_n-1); int tingkat1[50]; int tingkat2[50]; int tingkat3[50]; int tingkat4[50]; int i=2; int status=1; int tmp=1; tingkat2[1]=totient_n; tingkat2[2]=angka_random; /* matrix idntitas 1 0 0 1 */ tingkat3[1]=1; tingkat3[2]=0; tingkat4[1]=0; tingkat4[2]=1; gotoxy(x,y+2);printf("A[1,*]%5d%5d",totient_n,angka_random); gotoxy(x,y+3);printf("A[2,*]%5d%5d",tingkat3[1],tingkat3[2]); gotoxy(x,y+4);printf("A[3,*]%5d%5d",tingkat4[1],tingkat4[2]); int invers=0; //proses dan hasil while(status==1) { i++; x=x+9; tingkat1[i]=(tingkat2[i-2]/tingkat2[i-1]); gotoxy(x+10,y+1);printf("%5d",tingkat1[i]); tingkat2[i]=tingkat2[i-2]-tingkat2[i-1]*tingkat1[i]; tmp=tingkat2[i]; /*tmp untuk menyimpan hasil tingkat2[i] untuk membandingkan dengan 0 hingga dapat diketahui nilai status*/ if(tmp==0) { status=0; } gotoxy(x+10,y+2);printf("%5d",tmp);//yang ditampilkan hasil tingkat2[i] if(status!=0) { tingkat3[i]=tingkat3[i-2]-tingkat3[i-1]*tingkat1[i]; gotoxy(x+10,y+3);printf("%5d",tingkat3[i]); tingkat4[i]=tingkat4[i-2]-tingkat4[i-1]*tingkat1[i]; gotoxy(x+10,y+4);printf("%5d",tingkat4[i]); invers=tingkat4[i]; } } gotoxy(3,y+7);printf("invers adalah :%d",invers); if(invers<0) { gotoxy(3,y+8);printf("jika invers minus, maka invers = invers + totien_n;"); invers=invers+totient_n; gotoxy(3,y+9);printf("invers adalah :%d",invers); } getch(); }

berikut adalah hasil compile program di atas :

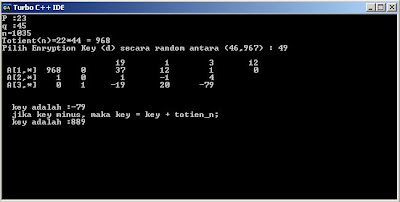
Jika hasil invers minus, maka invers+totient(n), seperti gambar di bawah ini :

Note : Key pada hasil compile tersebut adalah invers, maaf ada sedikit kesalahan pada saat posting topik ini :)